Guía de conocimientos EXANI-II Pensamiento matemático. Parte 1

Como dije en mis consejos para este examen es necesario estudiar la guía con todos sus temas en la ´parte de examen de admisión, aquí yo te presentare lo más importante de cada tema que debes de recordar para pasar el examen. Lo organizare igual que la guía para que no haya confusión. En esta primera parte de la guía pondré solo los temas de Pensamiento Matemático.

1.1.1 Jerarquía de operaciones básicas.

1.1.1.1 Operaciones combinadas de suma, resta, multiplicación y división  con números enteros

Como yo creo que todos saben sumar, restar, multiplicar y dividir, aquí el único detalle que todo el mundo se equivoca a la hora del examen es saber que realizar primero si hay sumas restas y multiplicaciones en diferentes paréntesis, es decir, tener algo como esto: 5((5-4+(5*8)-4)*8), sino sabes que hacer en estos casos esto es muy sencillo. Cuando uno tenga una operación como la anterior deberá empezar siempre por el paréntesis más centrado de la operación que en el ejemplo sería la multiplicación de (5*8) que una vez realizado se tendrá que realizar el paréntesis que se encuentre afuera del antes hecho, es decir, (5-4+40-4) como vez aquí yo ya he puesto el resultado del primer paréntesis realizado. Bueno después de realizar el segundo paréntesis pasamos al siguiente, recordando que ya debemos de tener el resultado del anterior paréntesis, y quedaría de la siguiente forma: (39*8). Y pasamos al fin al ultimo número que queda y está por fuera de todos los paréntesis y como este no tiene un signo de suma ni resta ni división, pasa directamente a ser una multiplicación entre el numero sacado anteriormente y el de afuera de esta manera nos queda entonces: 5*312 o 5(312), de esta forma terminamos la operación combinada del ejemplo. Entonces de lo anterior dicho recuerda que en una operación combinada con paréntesis siempre se empieza por el más centrado que haya en la operación y después se desarrolla siguiendo el orden de los paréntesis que le sigan.

Ahora te pondré otra situación que casí nunca se presenta en el examen, pero sirve en otras situaciones, en una operación sin paréntesis como la siguiente: 5+8*8/4-3, esta se realizara por jerarquía de signos de operación dice que la multiplicación sería la que tiene más valor en una operación combinada, luego iría la división, después la suma y por ultimo la resta. Y a que sabemos esto entonces en nuestro ejemplo empezamos por la multiplicación que sería 8*8, después de realizarla pasamos a la división 64/4, luego a la suma de la operación 16+5 y terminamos con la resta 21 - 3, quedaría entonces 18, sí no me crees realizalo en una calculadora tal y como la puse al principio para que veas que estoy en lo correcto. De lo dicho anterior te recomiendo pues recordar  la regla de jerarquía de operaciones *, /, +, - (si hubiera una potencia de cualquier número está se haría antes que todas las demás) .

1.1.1.2 Problema con suma, resta, multiplicación y división de con números decimales y fraccionarios.

Lo visto en el anterior tema sirve también para este otro tema, solamente para lo que es las operaciones, pero lo que debes de saber también de este tema es lo siguiente:

A) Operaciones de fracciones: Las operaciones de fracciones son muy importantes para el examen y si de verdad no te acuerdas de nada sobre de esto, primero te presentare las partes de una fracción. 

Supongamos que tenemos una fracción A / B el número o bien la letra A representa el numero que va ser dividido y este se le conoce como numerador, el número o letra B representa el número que divide al número A y se le conoce como denominador. Ahora que ya sabes las partes de una fracción ahora si pasamos a las operaciones que hay para esta:

        1)  La suma o resta de fracciones: Cuando hacemos sumas o restas de fracciones hay dos casos que se nos pueden presentar.

          I.- El primero es al tener una suma de dos fracciones o más con el mismos denominador, ejemplo 5/8 + 4/8, en este ejemplo vemos claramente que el denominador valor 8 para las dos fracciones y entonces hacemos directamente la suma de los numeradores sin cambiar el denominador, es decir que en el ejemplo quedaría lo siguiente: 5/8 + 4/8 = 9/8. Sí en el anterior ejemplo, el signo fuera cambiado por el de una resta se haría lo mismo, que sería realizar la resta de los numeradores conservando el mismo denominador, como lo siguiente: 5/8 - 4/8 = 1/8. Entonces recordemos de aquí que para realizar la sustracción o suma de fracciones con el mismo denominador, debemos de realizar la operación directamente en los numeradores sin cambiar el denominador.

                  II.- El segundo caso sería tener una operación de suma o resta con fracciones de diferentes denominadores como el siguiente ejemplo 5/4 +4/8 en este caso tenemos dos denominadores 4 y 8 hay dos formas de realizar esto. 

La forma fácil es de encontrar el común denominador de los dos para esto debes de encontrar un solo número que sea divisibles entre los dos denominadores o hacer el común múltiplo de los dos números, que sino lo sabes hacer lo mejor es buscar el número que sea divisible entre los dos números. En el ejemplo es muy fácil, ya que tenemos en las mismas fracciones el común denominador, pues 8 es divisible entre 8 y 4, nos da un numero entero en las dos divisiones. Ahora que he encontrado el común denominador lo pongo de la siguiente manera: 5/4 + 4/8 = ... + ... /8 y para encontrar los dos nominadores que faltan debemos primero dividir el común denominador entre el primer denominador de la primera fracción, en el ejemplo es 5/4 entonces dividimos el 8 entre 4. Una vez hecho esto multiplicamos lo sacado en la anterior división por el numerador de la misma fracción, de nuevo en el ejemplo quedaría de la siguiente forma: 2 que es el número resultante de la división lo multiplicamos por 5 ya que es el numerador de la fracción 5/4 lo que nos salga es el numero que pondremos en el primero de los espacios vacíos 10 + ... /8. Realizamos el siguiente espacio vacío con el mismo procedimiento antes hecho pero con la otra fracción de 4/8. Entonces, otra vez hacemos el mismo procedimientos que resumido sería dividimos el denominador común entre el denominador de la fracción, lo resultante lo multiplicamos por el numerador de la fracción y lo dado lo ponemos en el espació restante que quedaría así: 10 + 4 /8 = 14/8. Por ultimo debemos de reducir esta fracción, para reducirla debemos de encontrar el mínimo común divisor de los números de la fracción o bien el numero que pueda dividir a los dos números en este caso el  2, luego dividimos los dos números de la fracción por el 2, es decir 14 entre 2 y 8 entre 2 y lo resultante es el resultado final que es 7/4. 

SEA CUALQUIER MÉTODO DE ENCONTRAR EL COMÚN DENOMINADOR PARA SACAR LA SUMA O RESTA DE FRACCIONES SIEMPRE SERA DE ESTA MANERA.

La forma difícil es encontrar el común denominador multiplicando los dos denominadores de las fracciones en el ejemplo anterior: 5/4 + 4/8 sería 4*8= 32 y bien 32 es el común denominador. Después ser realiza otra vez el mismos procedimiento con cada fracción para sacar los dos espacios pero ahora con el común denominador de valor de 32 . Entonces recuerda para sacar los dos espacios de los numeradores que se suman debemos de dividir el común denominador entre los dos denominadores de las fracciones, después multiplicar los dos números resultantes por los nominadores de las fracciones, cada con su semejante y lo resultante lo pones en los dos espacios vacíos. 

Quedando en el ejemplo: 40 + 16 /32 = 56/32. Aquí es donde se encuentra la dificultad ya que debemos de reducir esta fracción a su mínima expresión y como los numero son muy grandes debemos de encontrar un numero exacto que sea divisible entre los dos este en el caso de que no sepamos sacar el mínimo común divisor es cuando se pone difícil. Bueno al final debemos encontrar que 8 es divisible entre los dos números de la fracción y al dividirlos 56 entre 8 y 32 entre 8, y nos queda 7/4 igual que el otro método.

        2)Multiplicación de fracciones: La multiplicación de fracciones es muy sencilla ya que lo único que se hará, es multiplicar el numerador de la primera fracción por el numerador de la segunda, y el denominador de la primera fracción* por el denominador de la  segunda fracción.

En un ejemplo quedaría así : 7/8 * 8/4 = 7*8 / 8*4 = 56/32. Sí en el examen te piden reducir ya sebes que debes de buscar un número que divide a los dos números de la fracción.

        3) División de fracciones: La división de fracciones es también sencilla solo debes de multiplicar de forma cruzada.

En ejemplo sería entonces: 8/9 / 5/4 = 8*4 / 9*5= 32/45. Sí en el examen te piden reducir ya sebes que debes de buscar un número que divide a los dos números de la fracción.

Por la parte de fracciones creo que ya es suficiente, aun nos falta estudiar un punto sobre las operaciones con decimales y esto es lo siguiente que he olvidado y que valía la pena decir en este y en el anterior es la regla de los signos en operaciones. 

1) La regla de los signos en sumas y restas: Sea en enteros o decimales, es decir, números con punto decimal, la propiedad de la regla de los signos en suma y resta, dice que según el valor que tenga cada numero de diferente signo el mayor siempre predominara y su signo se pondrá.

En esta imagen se ve que como lo dicho antes el valor de c, que es negativo, es mayor que el de a y b, y por ello el resultado es negativo.

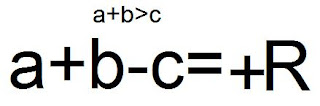En esta otra imagen se ve lo contrario de la anterior imagen ahora tanto a y b, que son positivos, es mayor que c, y por ello el resultado es positivo.

Un ejemplo de esto sería: 5+1-8= -2, como vimos antes 5+1<8, donde 8 es negativo, y por ello el resultado es negativo.

2) La regla del signo en multiplicación o división: Sí puse la regla del signo de la operación multiplicación y división es que las dos son iguales aquí hay dos propiedades a aprender:

       I.- En multiplicaciones o divisiones, si se multiplican o dividen entre valores de signos iguales y positivos, el resultando será entonces positivo.

Como antes se dijo cuando se multiplica o divide entre varios números positivos el resulta será siempre positivo.

          II.- En multiplicaciones o divisiones, si se multiplican o dividen entre valores de signos iguales y negativos, hay dos resultados posibles.

               a) Sí el número de valores, que se multiplica o dividen, es par, el resultado será entonces positivo.

En esta imagen se ve que el numero de valores negativos es par, entonces el resultados es positivo.

                  b) Sí el número de valores, que se multiplica o dividen, es impar, el resultado será entonces positivo

 

En esta imagen se ve que el numero de valores negativos es impar, entonces el resultados es negativo.

En estos no pienso poner ejemplos puesto que no lo creo necesario.

3) La regla de los signos de las potencias (esto no van a preguntarte pero tal vez te sirva algún día): en una potencia el resultado de un valor positivo será siempre positivo, pero si el valor que se eleva a la potencia de algún exponente, es negativo entonces las cosas cambian.

Estas reglas se asemejan a la de la multiplicación:

             a) Sí el exponente de la potencia es par, el resultado será entonces positivo.

             b) Sí el exponente de la potencia es impar, el resultado será entonces negativo

Igual que el anterior no creo que sea difícil entonces no pondré ejemplos

1.1.2 Relaciones de proporcionalidad.

1.1.2.1 Problemas con razones.

La razones son una forma de representar una comparación entre dos objetos, estas sirven para describir una relación de proporcionalidad que se pueda después comparar con otra razón, entonces para que queremos saber que es una razón si me puedo pasar directamente a la proporcionalidad directa y inversa, esto solo sirve para saber como acomodar los datos de algún ejercicios de proporcionalidad. Una razón se puede poner de diferente forma a/b o a:b estas dos formas son iguales y no cambian en nada, la razón se puede interpretar de la siguiente forma a es igual a b y casí siempre en un problema no vendrá de esta forma ya que uno debe de interpretarla.

Ejemplo: En un salón de clases hay 10 niñas y 5 niños ¿Como se puede representar los dos anteriores datos en forma de razón? 

Si 10 niñas es 5 niños, entonces la razón es 10:5 o 10/5

Les repito este tema es solo para complementar el siguiente lo que tiene que aprenderse es la manera de interpretar datos de un problema en forma de razón.

1.1.2.2 Problemas con proporciones.

Como antes lo comente cuando hablamos de proporciones directas e inversa y para saber que significa cada una de ellas las explicare.

1) Proporción directa: La proporción directa es cuando un objeto que se relaciona con otro aumenta o  disminuye de manera igualitaria. Por ejemplo, en un concierto que cobran, cuando aumenta la gente, las ganancias también aumentaran, esto es una proporcionalidad directa ya que los objetos aumentan.

2) Proporción inversa: La proporción inversa es cuando un objeto que se relaciona con otro aumenta mientras que el otro disminuye o disminuye mientras que el otro aumenta. Por ejemplo, en una pastelería mientras más se venda los pasteles, estos disminuirán pero las ganancias aumentaran. 

Ahora como se utiliza en un ejercicio para sacar datos de otros.

Para saber como utilizar esto te pondré un ejemplo de ejercicios de proporción. 

En la escuela de Tania se venden brownies, si hasta ahorita se lleva una ganancia de $25 por 30 de estos, ¿Cuánto se obtendrá al vender todos los brownies si en total hay 1500 de estos?

Para esto primero encontramos las razón enunciada en el problema que sería 30 es igual a $25, entonces 30/25 o 30 : 25, y    1500 brownies son igual a x, que es lo que buscamos, entonces 1500/x o 1500 : x. 
Ya que sabemos las razones las igualamos. 
30/25 = 1500/x 
Después despejamos de tal manera que la incógnita o bien lo que busquemos quede de un lado y las operaciones del otro.
x= 1500*25 /30
Y resolvemos.
Como x= $1250, entonces podemos concluir que la ganancia total será de $1250.

Por ahora solo realizare este tema si pusiera todo en un solo documento sería brumador y muy cansado. pero te lo aseguro que con esto tienes lo suficiente para realizar los ejercicios de estos temas.